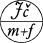Tutorial Track
A. Brooke-Taylor: Large cardinal axioms in category theory and its applications
The theory of accessible categories was developed to provide a kind of category-theoretic version of model theory. It turns out that large cardinal axioms have a major role to play in this theory, with "reflecting down" properties of large cardinals giving structure theorems for various subcategories of accessible categories. More recently this has flowed on to give applications of large cardinals in other areas of mathematics, for example in algebraic topology in the 2000s and in the study of Abstract Elementary Classes in model theory in the 2010s. In this tutorial I will give an introduction to accessible categories with an emphasis on the influence of set theory.
slides I, slides II, slides IIIM. Elekes: Problems and techniques concerning the Baire function classes
The Baire function classes are defined starting from the continuous functions and recursively taking closures under pointwise limits. One of the main motivation for studying them comes from the fact that the union of the Baire classes is the class of Borel functions.
In their seminal paper Kechris and Louveau defined three very important and natural rank functions (ordinal-valued functions) on the first Baire class. Our first topic, motivated by paradoxical geometric decompositions, will be the extension of this theory to the higher Baire classes, and also to show that their assumption of the compactness of the underlying space can be dropped.
The second topic we discuss is a solution to a problem due to Laczkovich: What are the possible order types of the linearly ordered subset (under the pointwise ordering) of the first Baire class? What makes this class particularly interesting is that the continuous case is well-known and the case of higher Baire classes is independent of ZFC.
There will be emphasis on more advanced techniques used to handle these problems, in particular on class-by-class topology refinements.
O. Guzman: On $\mathfrak{a},\mathfrak{b}$ and $\mathfrak{s}$
The Cardinal invariants of the continuum are certain cardinal numbers that are bigger than $\omega$ and smaller or equal than the cardinality of the real numbers$.$ The main interest is when they have some nice combinatorial or topological definition. Currently, there is a long list of cardinal invariants that is being studied and compared by set theorists. The numbers $\mathfrak{a},$ $\mathfrak{b}$ and $\mathfrak{s}$ are three of the most well known cardinal invariants. Let's recall the definitions:
1) Let $f,g\in\omega^{\omega}$, define $f\leq^{\ast}g$ if and only if $f\left( n\right) \leq g\left( n\right) $ holds for all $n\in\omega$ except finitely many. We say a family $\mathcal{B}\subseteq\omega^{\omega}$ is unbounded if $\mathcal{B}$ is unbounded with respect to $\leq^{\ast}$.
2) The bounding number $\mathfrak{b}$ is the smallest size of an unbounded family.
3) We say that $S$ splits$X$ if $S\cap X$ and $X\setminus S$ are both infinite. A family $\mathcal{S\subseteq}$ $\left[ \omega\right] ^{\omega}$ is a splitting family if for every $X\in\left[ \omega\right] ^{\omega}$ there is $S\in\mathcal{S}$ such that $S$ splits $X.$
4) The splitting number $\mathfrak{s}$ is the smallest size of a splitting family.
5) A family $\mathcal{A}\subseteq\left[ \omega\right] ^{\omega}$ is almost disjoint (AD) if the intersection of any two different elements of $\mathcal{A}$ is finite, a MAD family is a maximal almost disjoint family.
6) The almost disjointness number $\mathfrak{a}$ is the smallest size of a MAD family. It is known that $\mathfrak{b\leq a}$ and there is no other provable relation between them. While the consistency of $\mathfrak{s<b}$ is easy, the consistency of the inequalities $\mathfrak{b<s}$ and $\mathfrak{b<a}$ are much harder. In this tutorial, we will (hopefully) see a full proof of the consistency of such inequalities. If there is time, in the end, we will see some other inequalities, like $\mathfrak{u<a}.$
slides I, slides II, slides IIIA. Medini: Topological applications of Wadge theory
Wadge theory provides an exhaustive analysis of the topological complexity of the subsets of $2^\omega$. Fons van Engelen pioneered its applications to topology by obtaining a classification of the zero-dimensional homogeneous Borel spaces (recall that a space $X$ is homogeneous if for all $x,y\in X$ there exists a homeomorphism $h:X\longrightarrow X$ such that $h(x)=y$). As a corollary, he showed that all such spaces (apart from trivial exceptions) are in fact strongly homogeneous (recall that a space $X$ is strongly homogeneous if all non-empty clopen subspaces of $X$ are homeomorphic to each other).
In a joint work with the other members of the “Wadge Brigade” (namely, Raphaël Carroy and Sandra Müller), we showed that this last result extends beyond the Borel realm if one assumes AD (that is, the Axiom of Determinacy). We intend to sketch the proof of this theorem, with a view towards a complete classification of the zero-dimensional homogeneous spaces under AD. At the same time, we hope that the tutorial (more precisely, some initial segment of it) might serve as an introduction to Wadge theory and to homogeneity, in the context of zero-dimensional spaces.
slides I, slides II, slides III